The Runge-Kutta method is one of several numerical methods of solving differential equations. Some systems motion or process may be governed by differential equations which ar e difficult to. What about a code for Runge Kutta method for second order ODE. Something of this nature: d^2y/dx^2 + 0.6*dy/dx 0.8y = 0.
i'm trying to code a simple runge-kutta method
Below is my 4th order Runge-Kutta algorithm to solve a first order ODE. /* This code is a 1D classical Runge-Kutta method. Compare to the Wikipedia page. The task apparently asked for the 4th order classical Runge-Kutta method of the first tableau. – LutzL Mar 17 '17 at 12:14 @PeterSM.
The function to be approximated and the runge-kutta method are separate definitions, which are called within the loop in the main function.
approximate solutions for y and t are pushed into a separate vectors.
I'm receiving the following errors and struggling to figure out why:Error message snapshot
The code:
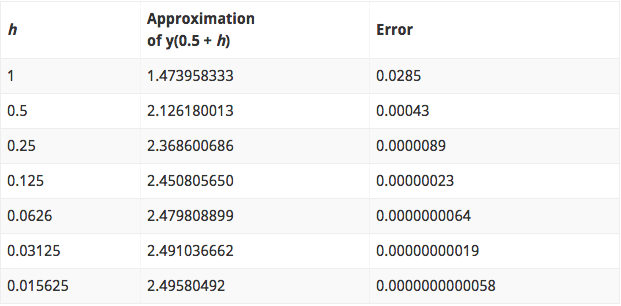
Runge Kutta Example
Hariom Singh1 Answer
If you want to use multiple return you can use std::tuple
And returned value can be captured
Error fixed code
 drescherjm
drescherjmFirst Order Runge Kutta Method
Hariom SinghHariom SinghPython Runge Kutta 4th Order

Not the answer you're looking for? Browse other questions tagged c++c++11runge-kutta or ask your own question.
- concentration
- species
In other words, X[species i][location j] - that is TWO dimensions.
What you are describing above seems to be the TERMS which COUPLE those equations, which could actually be read, stored and used as a ONE-dimensional array of structs; e.g.
struct process{ int species, in, out; double value; }. When you read them, just assign them sequentially to a vector of structs using push_back(). When you use them in the derivative function just go through them one by one.
If , as I suspect, t is time, you should not be storing that - you should dump your X to file at identified intervals.
It is unclear what you mean by 'convergence'. This version of RK is explicit: there is no in-step iteration. If you meant convergence to final steady state then just use the normed distance between successive values of your dependent-variable array.
I think you need to write down your original equations.